Рассмотрим пример простейшего дифференциального оператора второго порядка
действующего на вещественные функции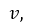 
которые обладают следующими свойствами:
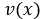определены в области 
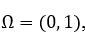они непрерывны и дважды дифференцируемы во всех внутренних точках этой области;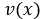- квадратично суммируемы на
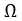вместе со своими производными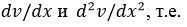 
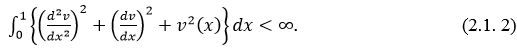
Известно, что вещественные функции 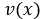, обладающие свойством 
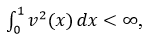, образует гильбертово пространство функций 
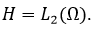. Далее предположим, что функции 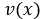принимают заданные значения на границе области 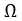при 
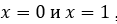, например
. 
Обозначим множество функций 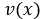, удовлетворяющих условиям a), b) и (2.1.3), через 
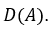. Будем называть это множество областью определения оператора 
.
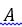Для функци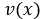й и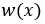 
в гильбертовом пространстве 
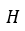с областью определения 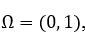введем в рассмотрение скалярное произведение
Подействуем теперь оператором 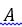на функцию 
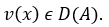. В результате будем иметь новую функцию 
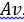, также определенную в 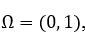и принадлежащую 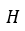. Рассмотрим скалярное произведение функци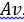и и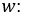 
И проинтегрируем полученное выражение (2.1.5) по частям, тогда
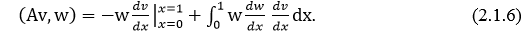
Внеинтегральный член в правой части (2.1.6) обращается в нуль в силу того, что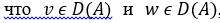 
, а каждая функция этого множества по предположению (2.1.3) равна нулю на границах интервалов. В результате соотношения (2.1.6) перейдет в следующее:
Интеграл в (2.1.7) еще раз возьмем по частям. Получим
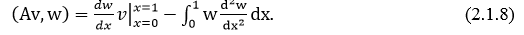
Внеинтегральный член в этом соотношении в силу условия (2.1.3) также обратиться в нуль. И в результате мы будем иметь
. 
Сравнивая соотношения (2.1.5) и (2.1.9), мы приходим к выводу, что
Выражение (2.1.10) является тождеством Лагранжа для симметричных операторов. Иначе говоря, если для функций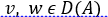 
имеет место равенство (2.1.10), то оператор A является симметричным. Оператор A можно назвать также формально самосопряжённым.