Марчук Г.И. Сопряженные уравнения и анализ сложных систем
СОПРЯЖЕННЫЕ УРАВНЕНИЯ И ИХ ФУНКЦИОНАЛЫ
Перейдем к рассмотрению основных и сопряженных уравнений с источниками. Начнем с простейших примеров. Рассмотрим задачу
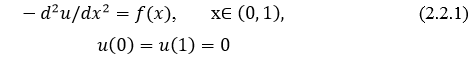
Пусть решение задачи (2.2.1) 
принадлежат множеству 
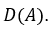, а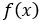 
принадлежит 
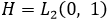– пространству вещественных интегрируемых с квадратом функций. Оператор
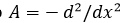на функциях 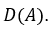из является симметричным. Решение задачи нетрудно получить в явном виде:
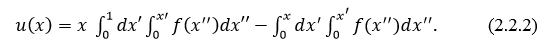
Предположим, что нам требуется знание не самого решения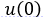 
в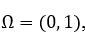 
, а лишь конкретного функционала от этого решения. Пусть это будет
где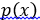 
– характеристика прибора или измерения. Например, если
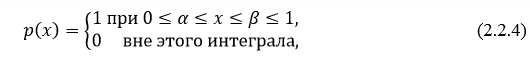
то это означает что прибор интегрирует значение решения лишь в интервале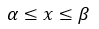 
и не реагирует на решение в оставшейся части интервала.
Теперь покажем, что тот же функционал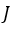 
можно получить на основе специальным образом сформулированной сопряженной задачи. В самом деле, рассмотрим сопряженную задачу
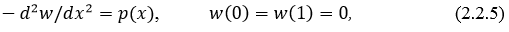
где 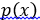определено в функционале (2.2.3). Будем считать, что 
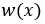принадлежит тому же множеству 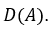, что и решение основной задачи. Тогда умножим уравнение из (2.2.1) на 
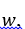, уравнение из (2.2.5) на 
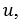, результаты вычтем один из другого и проинтегрируем по всей области определения решения:
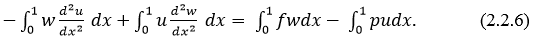
Интегрированием по частям дважды одного из членов в левой части (2.2.6) с учетом граничных условий легко показать, что левая часть равна нулю. Это получаем и непосредственно, имея в виду тождество Лагранжа. Тогда (2.2.6) переходит в следующее соотношение:
Но второй член в (2.2.7) является искомым функционалом. Тогда две эквивалентные формулы для его определения имеют вид:
Таким образом, мы получили двойственную формулу для определения одного и того же функционала. Во многих сложных задачах оказывается более предпочтительно пользоваться второй формулой из (2.2.8), особенно в тех случаях, когда функция источника 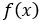и в вариациях задачи меняется, а оператор и граничные условия остаются прежними.Рассмотрим теперь на нашем простейшем примере проблему чувствительности 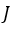функционала источнику 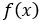. С этой целью предположи
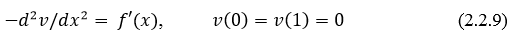
Здесь предположим, что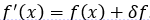 
. Поскольку задача (2.2.9) линейна, то ее решение имеет вид
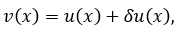
где штрихом обозначается возмущенная функция. Тогда для вариаций функционала в формуле
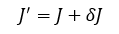
получим два эквивалентных соотношения:
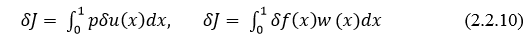
Вторая из формул (2.2.10) замечательна тем, что позволяет непосредственно связать вариацию источника в основной задаче с вариацией исследуемого функционала. Кроме того, для этого не нужно решать возмущенную задачу (2.2.9) и находить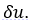 
. Здесь 
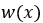играет роль весовой функции, которая ответственна за чувствительность функционала. В связи с этим сопряженную функцию 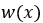иногда называют функцией ценности информации или просто ценностью.
Важно отметить, что при введенных функционалах исходные задачи даже с самосопряженными операторами порождают задачи просто сопряженные. Такие задачи удобно называть сопряженными по отношению к выбранным функционалам.
1. Тестовая задача для разработки класса метода прогонки
Рассмотрим простейший пример при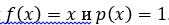 
. Тогда основная задача (2.2.1) имеет вид
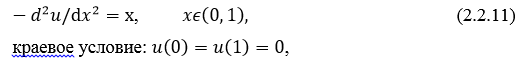
и нам требуется вычислить функционал (2.2.3):
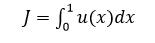(2.2.12)
2. Пусть далее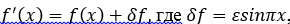 
где , тогда возмущенная задача (2.2.9) примет вид
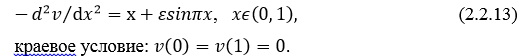
3. Сопряженная задача (2.2.5) для 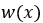в данном случае имеет вид
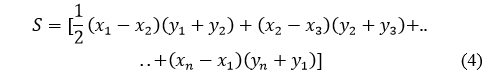
Далее для вычисления поправки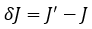 
можно использовать формулы
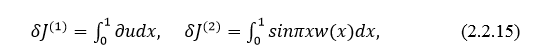
где 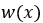– решение сопряженной задачи (2.2.14).
Предложенные тестовые примеры (2.2.11, 2.2.13, 2.2.14), взяты из книги «Сопряженные уравнения и анализ сложных систем» Марчука. Легко увидеть, что они имеют аналитическое решение. Поэтому их удобно использовать в качестве тестов при проверке решений методом прогонки, для которого в дальнейшем создадим визуальный проект.
Применяя разностные схемы и используя метод прогонки в данной работе решены три задачи: основная, возмущенная, сопряженная.
Решения прямой и сопряженной краевых задач необходимы для вычисления значений функционалов (2.2.15). Ниже будет показано, что полученные решения совпадают с результатами полученными в книге «Сопряженные уравнения и анализ сложных систем».